Orthogonal Matrices and Gram-Schmidt

June 4, 2019

Orthonormal vector: Vectors $q_1,q_2…,q_n$ are orthonormal iff

This is saying these vectors are orthogonal to all the others, and they are normalized to have length one (unit vector). One example is $\begin{bmatrix}1&0&…&0\end{bmatrix}, \begin{bmatrix}0&1&…&0\end{bmatrix},..,\begin{bmatrix}0&0&…&1\end{bmatrix}$. But note that this is not the only example. Let the matrix

Then

You can call the matrix $Q$ orthonormal matrix, which is a less known name. But when $Q$ is square, it’s an Orthogonal Matrix. The orthogonal matrix has the following property

Some examples of $Q$ are permutation matrix $P_{ij}$ , or

Projection into C(Q)

As long as we use the notation $Q$, it implies that the columns of $Q$ are orthonormal, but not necessary unit vectors. Recall from our projection matrix formula:

And recall when a matrix $A$ is full rank, $A^\top A$’s inverses can be factored out and we got identity matrix on $P$. This is saying we are projecting into nowhere, the vector is staying at the original space. $Q^\top Q$ is by definition equal to $I$; and when $Q$ is square/$Q$ is an orthogonal matrix, $Q(Q^\top Q)^{-1}Q^\top=QQ^{-1}Q^{\top-1}Q^\top=I$ . And remember $A^\top A\hat{\mathbf x}=A^\top \mathbf b$,

Gram-Schmidt

Let’s try to make a matrix’s columns orthonormal. For two arbitrary vectors $\mathbf {a,b}$, we want to find $a',b'$ s.t. $a'\perp b'$. And $a', b'$’s unit vectors are $q_1,q_2$ . To do so we need projections. Remember projected vector $\mathbf p$ is onto the space of $A$, and there’s an error/difference $\mathbf e=\mathbf b -\mathbf p$. This error is in the $N(\mathbf a^\top)$, and it is perpendicular to the projected vector. This is what we want. (In this case $a=a'$)

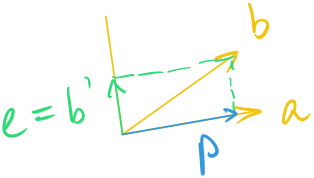
To verify, $a^\top b'$ should be equal to 0:

This can be generalized from vectors $\mathbf{a,b}$ to a plane or a space.

A =QR

…