Projection Matrices and Least Squares

June 3, 2019

Remember our projection matrix $P$ is

$P=A(A^\top A)^{-1}A^\top$

Prop. 1 If $\mathbf b$ in column space, $P\mathbf b=\mathbf b$;

Prop. 2 If $\mathbf b$ perpendicular to column space, $P\mathbf b=0$.

Let’s solve Prop. 2 First. What vectors are in perpendicular to the null space of $A$ ? From lecture 14, we knew that $R(A)\perp N(A)$ . One shall easily infer from that $C(A)\perp N(A^\top)$ . Therefore the vectors in the left nullspace of $A$ are perpendicular to its column space. If $\mathbf b$ in $N(A^\top)$ , then $A^\top \mathbf b=0$ immediately, and

$\mathbf p=P\mathbf b=A(A^\top A)^{-1}A^\top \mathbf b=0$

because we have $A^\top \mathbf b=0$ on the very right.

Coming back to Prop. 1, what is $\mathbf b$ if it is in the column space of $A$ ? It’s $A\mathbf x$ . Then

$\begin{align} P\mathbf b&=A(A^\top A)^{-1}A^\top A\mathbf x\\ &=A[(A^\top A)^{-1}A^\top A]\mathbf x\\ &=A\mathbf x \end{align}$

$A\mathbf x$ is just $\mathbf b$ .

Figure 1. Geometric view of vector b projecting into A's column space, with projected vector p and e as the difference

Geometrically, $\mathbf e=\mathbf b-\mathbf p$ , $\mathbf e$ is also a projection, but it’s just projected into the left nullspace. What’s the projection matrix for $\mathbf e$ ? It is obvious when we expand $\mathbf p+\mathbf e=\mathbf b$ :

$\begin{align} \mathbf p+\mathbf e&=\mathbf b\\ P\mathbf b+\mathbf e&=\mathbf b\\ P\mathbf b+(I-P)\mathbf b&=\mathbf b \end{align}$

Thus the projection matrix is just $I-P$ .

Least Square

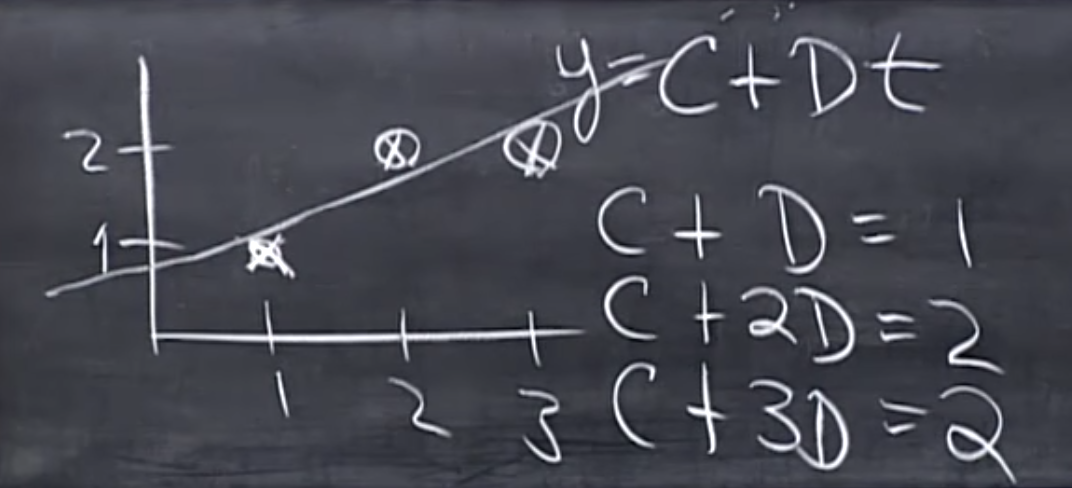
Now let’s turn to linear regression. To put it simple, linear regression is just to find a line that seems to fit a bunch of points well. But you know as long as the points are not in the straight line, we cannot have a line that perfectly goes through every points given. Therefore we need a criterion of what makes a “good” line. Here the criterion is the vertical distance between the line the points projected into the line, which would be clear a bit later.

Let’s do an example. Suppose the points’ coordinates are $(1,1), (2,2), (3,2)$ , we can substitute these points into a line’s equation $y=\beta_0+\beta_1t$ :

$\begin{align} \beta_0+\beta_1&=1\\ \beta_0+2\beta_1&=2\\ \beta_0+3\beta_1&=2\\ \end{align}$

it’s clear that there’s no line can solve these equations since only horizontal line goes through (2,2) and (3,2) but horizontal line does not go through (1,1). Rewrite the equations into matrix form, let $\boldsymbol\beta=[\beta_0,\beta_1]$ , the points x values being $\mathbf X$ and y values being $\mathbf y$ :

$\begin{align} \mathbf X\boldsymbol \beta&=\mathbf y\\ \begin{bmatrix} 1 & 1\\ 1 & 2\\ 1 & 3 \end{bmatrix}\begin{bmatrix} \beta_0\\ \beta_1 \end{bmatrix} &=\begin{bmatrix} 1\\ 2\\ 3 \end{bmatrix} \end{align}$

Since the equation is unsolvable, the only possible situation is that we solve the solvable ones, where $\mathbf y$ is projected into the column space of X, $C(\mathbf X)$. When $\mathbf y$ is projected into $C(\mathbf X)$ :

$\begin{align} \mathbf p&=\mathbf X\boldsymbol{\hat \beta}\\ \end{align}$

For $\boldsymbol{\hat \beta}$ is some random numbers and $\mathbf X\boldsymbol{\hat \beta}$ is just linear combinations of the columns of $\mathbf X$ . Then the error is, similar to before, the unprojected ($\mathbf y$) subtracting the projected,

$\mathbf e=\mathbf y-\mathbf X\boldsymbol{\hat\beta}$

The error is minimized when $\mathbf p=\mathbf X\boldsymbol{\hat \beta}$ is a vertical projection (refer to note 15 figure 1, p is the vertical projection of b) of $\mathbf y$ . This matches exactly (if you don’t know it’s ok) the square error statistician trying to solve:

$\begin{align} \lVert\mathbf y-\mathbf X\boldsymbol\beta\rVert_2^2&=\lVert\mathbf e\rVert^2 \end{align}$

Now let’s solve for the $\boldsymbol{\hat \beta}$ that can give us a vertical projection:

$\begin{align} \mathbf X^\top(\mathbf y-\mathbf X\boldsymbol{\hat\beta})&=0\\ \boldsymbol{\hat\beta}&=(\mathbf X^\top\mathbf X)^{-1}\mathbf X^\top \mathbf y \end{align}$

$\mathbf X^\top\mathbf X$ is invertible if and only if $\mathbf X$ is full column rank. When it won’t be full column rank? When we have too few points and it has too many columns (i.e. predictor dimension too high). Or we have enough points but some of them are dependent.