Matrix Spaces; Rank 1; Small World Graphs

May 29, 2019

Matrix Space

Last lecture we’ve talked briefly that a $3\times 3$ matrix $M$ is a vector space, because we can add, multiply by constant to “things” in the space. For “things” we used to use vectors. But right now we extend it to matrix, just because it can allow operations of adding and multiplying by constant. Or if you like, you can call the matrix vector. And the subspaces for this $3\times 3$ matrix are

$3\times 3$ symmetric matrix $S$
$3\times 3$ upper triangular matrix $U$
$3\times 3$ diagonal matrix $D$

What are the bases for these spaces?

There’re 9 numbers in $M$ , so we probably need 9 matrix to be the basis:

$\begin{bmatrix} 1 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{bmatrix}\rightarrow \begin{bmatrix} 0 & 1 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{bmatrix}\rightarrow \begin{bmatrix} 0 & 0 & 1\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{bmatrix}\rightarrow ...\rightarrow \begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 1 & 0 \end{bmatrix}\rightarrow \begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 1 \end{bmatrix}$

and $\dim M=9$ . This space is similar to $\mathbb R^9$ but written in a matrix instead of a column vector. For symmetric matrix $S$ ? The dimension for $3\times 3$ symmetric matrix is 6:

$\begin{bmatrix} 1 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{bmatrix} ,\begin{bmatrix} 0 & 1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 0 \end{bmatrix} ,\begin{bmatrix} 0 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 0 \end{bmatrix} ,\begin{bmatrix} 0 & 0 & 1\\ 0 & 0 & 0\\ 1 & 0 & 0 \end{bmatrix} ,\begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & 1\\ 0 & 1 & 0 \end{bmatrix} ,\begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 1 \end{bmatrix}$

For upper triangular $3\times 3$ matrix it’s still 6, one 1 for each location in the upper triangular. What about diagonal matrix? Diagonal matrix is just infact $S\cap U$ , and $\dim (S\cap U)=3$ , one 1 in each position on diagonal line. Remember we’ve talked about union is not a subspace(Lecture 6). So $S\cup U$ is not a subspace. But we can define a new opetaion $S+U$ that takes all possible sums of this two spacesI think it’s useful to imagine taking the sum of their bases, and

$S+U=M$

their sum is all the $3\times 3$ matrices.

Differential Equations

if you don’t want to look at this part just skip it, it’s about why we care about matrix as a vectorWhy we would like to take a matrix and call it a vector and think about its spaces? Let’s have a second order differential equations:

$y''+y=0$

Some solutions include

$y=\cos x,\ \ y=\sin x,\ \ \mathrm{and}\ \ y=e^{ix}$

the complete solution is

$y=c_1\cos x+c_2\sin x$

where $c_1$ and $c_2$ can be any real numbers. This complete solution is a vector space. Even though these don’t look like vectors, we can still add and multiply by a number to it. So they form a vector space. The basis for this space is $\cos x$ and $\sin x$ . The dimension is 2.

Rank 1 matrix

Let’s have a rank 1 matrix:

$A=\begin{bmatrix} 1 & 4 & 5\\ 2 & 8 & 10\\ \end{bmatrix}$

One interesting thing about rank 1 matrix is that $A=\mathbb{uv}^T$ where $\mathbf u$ and $\mathbf v$ are column vectors. That is:

$A=\begin{bmatrix} 1\\ 2\\ \end{bmatrix}\begin{bmatrix} 1&4&5\\ \end{bmatrix}$

rank 1 matrices are building blocks for more complex matrices.

Graph

This is the directed/undirected graph that CS-background students are familiar with

$G=\{nodes,edges\}$

We use a set of nodes and edges to represent a graph.

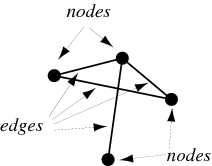
This will be further discussed in the next notes.