Laplace Transform solving jump discontinuities

The unit step function $H(t)$ is that

$H(t)=\cases{0,\ t<0\\1,\ t\geq0}\tag{1}$

Its graph is

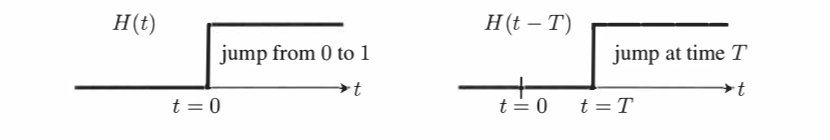
Figure 1. The unit step function and its shift

And we denote its shift by $H(t-T)$ or $H_T(t)$. Sometimes we also let $H(0)$ undefined just to make everyone happy.

There’s another that step up at time $t=a$ and step down at time $t=b$, making it a box, this function $u_{ab}(t)=H_a(t)-H_b(t)=H(t-a)-H(t-b)$.

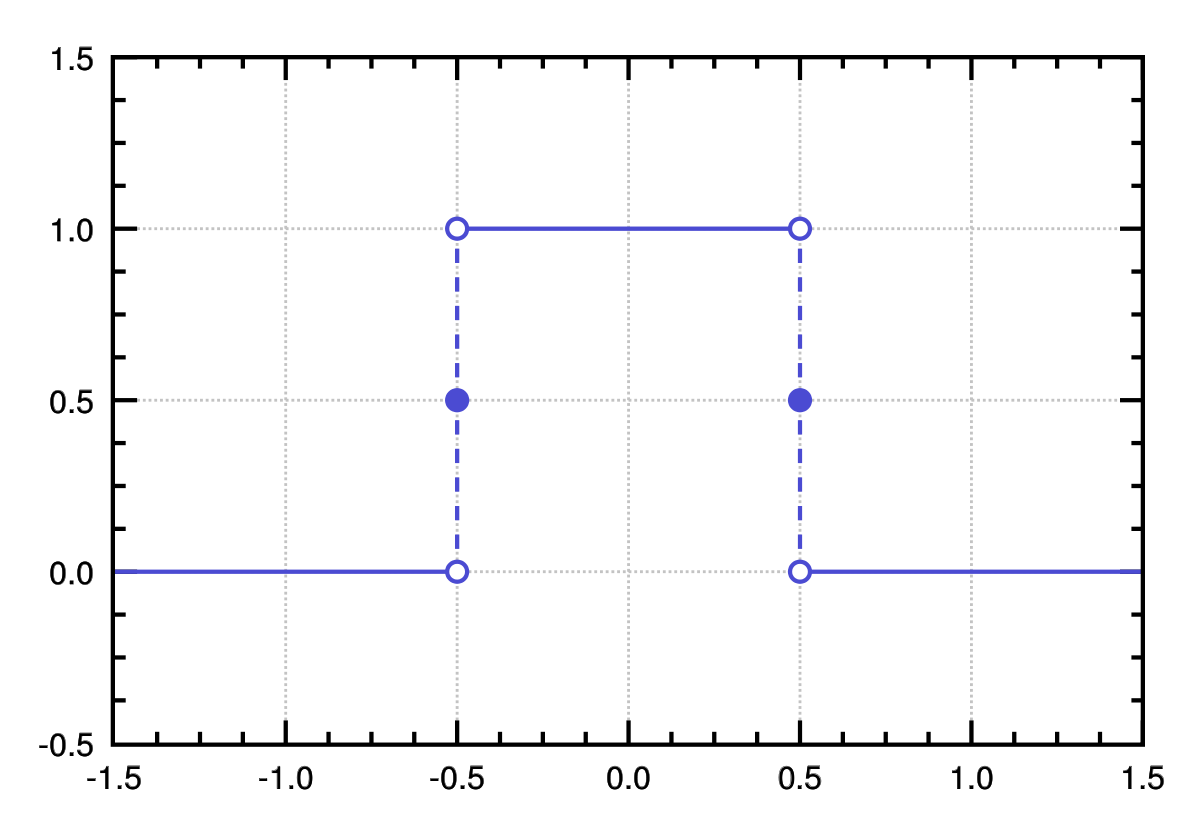
Why we care about such function? For example, if we want to find a Lapace transform on a function on certain interval $[a,b]$ we can multiply the function by $u_{ab}(t)$, like below

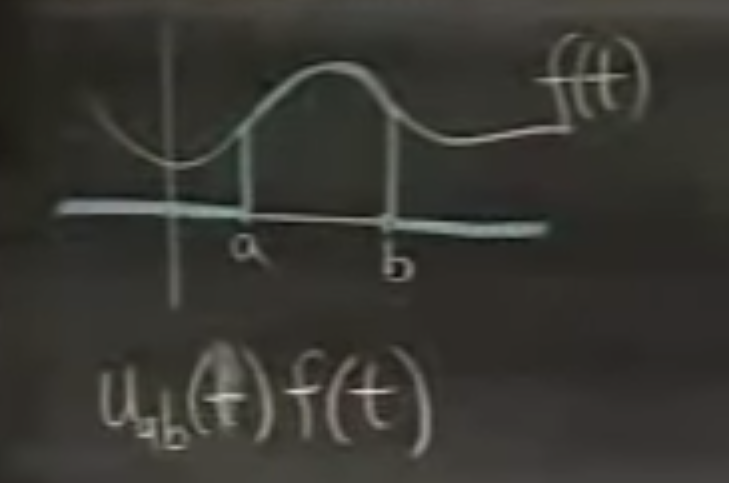
Figure 3. Step box function multiply f(t)

Unique Laplace transform w/ step functions

What’s the Laplace transform on the step function $H(t)$?

$\mathcal L(H(t))=\int_0^\infty \underbrace{H(t)}_{1,when\:t\geq0}e^{-st}\:dt=\frac{1}{s}$

This isn’t a big problem, but what’s $\mathcal L^{-1}(\displaystyle \frac{1}{s})$? Is it the constant 1 or the step function $H(t)$? This problem not only happens on these, but on all the functions.

Figure 4. Same Laplace transform on different functions

On Figure 4., $f(t)$ with different less-than-zero values. Because Laplace transform only cares about values greater than 0, $f(t)$ with different less-than-zero values has the same Laplace transform. Therefore we want to have a unique inverse Laplace transform. This is done by multiplying the $f(t)$ by step function $H(t)$.

First off, there’s no formula that can express $\mathcal L(f(t-a))$ in terms of $\mathcal L(f(t))$, because, as in Figure 5, Laplace transform of $f(t-a)$ use values that were not used in $f(t)$. When we do Laplace transform, we’ve already given away the information of the negative values. <assuming $a>0$ >

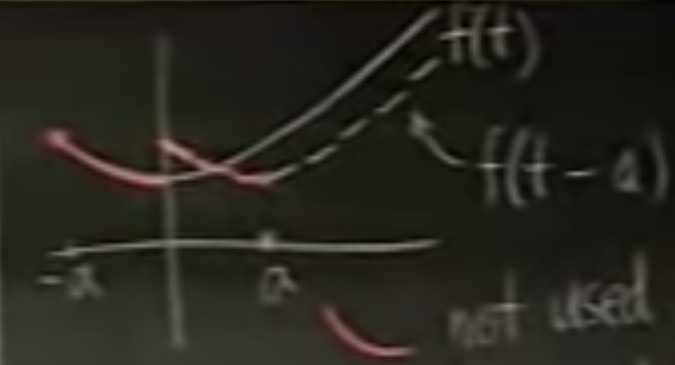
Figure 5. Negative values not used for shifted f(t)

What we can do instead is we have formulas for $\mathcal L(H(t-a)\cdot f(t-a))$ in which we erase away the original negative values, as in Figure 6.

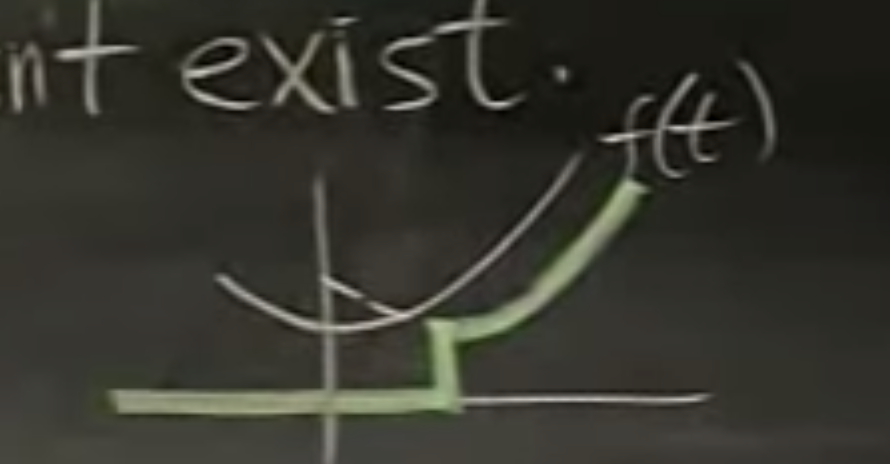
Figure 6. Shifted f(t) multiply step function

The formula for that is

$\begin{align} \mathcal L(H(t-a)\cdot f(t-a))&=e^{-as}F(s)\\ \end{align}\tag{2}\\$

But the problem is the functions in our problems will not appear in the form of $f(t-a)$ therefore we need another formula:

$\mathcal L(H(t-a)\cdot f(t))=e^{-as}\mathcal L(f(t+a))\tag{3}$

Proof for (2):

$\begin{align} \mathcal L(H(t-a)\cdot f(t-a))&=\int_0^\infty e^{-st}H(t-a)f(t-a)\:dt\\ &<let\ t_1=t-a>\\ &=\int_{-a}^\infty e^{-s(t_1+a)}H(t_1)f(t_1)\:dt\\ &=e^{-sa}\int_{-a}^\infty e^{-st_1}\underbrace{H(t_1)}_{0 \ if-a<0,1\ if-a>0}f(t_1)\:dt\\ &=e^{-as}\int_{0}^\infty e^{-st_1}f(t_1)\:dt\\ &=e^{-as}F(s) \end{align}$

From (2) to (3) we can brute force it by replacing $f(t-a)$ by $f(t)$ through $t=t-a$.

Laplace Transform solving jump discontinuities

Unique Laplace transform w/ step functions

Inverse Laplace