Introduction to Fourier Series

June 11, 2019

(Book 8.1)

Continuing from note 24 in Linear Algebra,

Aside from the trigonometric identity that $\displaystyle \sin^2(t)=\frac{1}{2}-\frac{1}{2}\cos2t$ , there’s another way we can get the orthogonality relation such as $\displaystyle \int_{-\pi}^{\pi}\cos(nt)\sin(mt)\:dt=0$ , we can use DE:

$x''+m^2x=0$

What satisfies this DE? $\sin(mt)$ and $\cos(nt)$ you may recall this DE from the undamped case. Let $u_m,v_n$ be any two different sin or cos functions, $m\neq n$ ,then

$\begin{align} u_m''&=-m^2u_m\\ v_n''&=-n^2v_n \end{align}$

And let’s take have the following:

$\begin{align} \int_{-\pi}^{\pi}u_m''v_n\:dt&=-m^2\int_{-\pi}^{\pi}u_mv_n\:dt\\ \int_{-\pi}^{\pi}u_mv_n''\:dt&=-n^2\int_{-\pi}^{\pi}u_mv_n\:dt\\ \end{align}\tag{1}$

And

$\int_{-\pi}^{\pi}u_m''v_n\:dt=u_m'v_n\vert_{-\pi}^\pi-\int_{-\pi}^{\pi}u_m'v_n'\:dt=-\int_{-\pi}^{\pi}u_m'v_n'\:dt\tag{2}$

through integration by parts and $u_m'v_n\vert_{-\pi}^\pi=0$ by listing out all possible cases that $u_m,v_n$ may take. And (2) is symmetric, this means we connect (2) to the two integrations in (1), we have:

$-m^2\int_{-\pi}^{\pi}u_mv_n\:dt=-n^2\int_{-\pi}^{\pi}u_mv_n\:dt$

For $m\neq n$ , this can only happens when $\displaystyle \int_{-\pi}^{\pi}u_mv_n\:dt=0$ . Only case left is $n=m$ , if $u_n=v_n=\sin\, or\, \cos$ we have nothing to prove because they are the same and evaluated to $\pi$ . If:

$\int_{-\pi}^{\pi}u_nv_n\:dt=\int_{-\pi}^{\pi}\cos nt\sin nt\:dt=1/2\int_{-\pi}^{\pi}\sin 2nt\:dt$

This finished the proof (what a mess).

Square-wave function

Let’s try to find the Fourier series for the square-wave function. It is on $[-\pi,\pi]$

$f(t)=\cases{ \begin{align} -1\quad &if\ -\pi<t<0\\ 1\quad &if\ 0<t<\pi\\ 0\quad&if\ t=-\pi,0,or\ \pi \end{align} }$

It has period $2\pi$ .

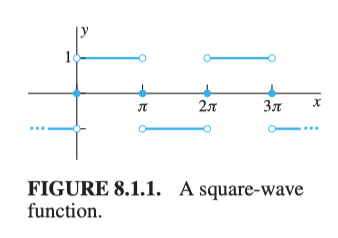
Since it is not continuous from $-\pi$ to $\pi$ nor from 0 to $2\pi$ , we need to separate the integration.

$\begin{align} a_n&=\frac{1}{\pi}\int_{-\pi}^{\pi}f(t)\cos nt\:dt\\ &=\frac{1}{\pi}\int_{-\pi}^{0}-\cos nt\:dt+\frac{1}{\pi}\int_{0}^{\pi}\cos nt\:dt\\ &=\frac{1}{\pi}\left[\frac{1}{n}-\sin nt\right]_{-\pi}^0+\frac{1}{\pi}\left[\frac{1}{n}\sin nt\right]_0^{\pi}\\ &=0 \end{align}$

And

$\begin{align} b_n&=\frac{1}{\pi}\int_0^{2\pi}f(t)\sin nt\:dt\\ &=\frac{1}{\pi}\int_{-\pi}^{0}-\sin nt\:dt+\frac{1}{\pi}\int_{0}^{\pi}\sin nt\:dt\\ &=\frac{1}{\pi}\left[\frac{1}{n}\cos nt\right]_{-\pi}^0+\frac{1}{\pi}\left[\frac{1}{n}-\cos nt\right]_0^{\pi}\\ &=\frac{1}{\pi n}(1-\cos n\pi)-\frac{1}{\pi n}(\cos\pi n-1)\\ &=\frac{2}{\pi n}(1-\cos n\pi)\\ &=\frac{2}{\pi n}(1-(-1)^n) \end{align}$

Therefore

$b_n=\cases{\begin{align} \frac{4}{\pi n}&\quad if\ n \ is\ odd\\ 0&\quad if\ n\ is\ even \end{align}}$

Remember $b_k$ is coefficients for $\sin kt$ , so the Fourier series for the square-wave function is

$f(t)=\frac{4}{\pi}\sum_{n\ odd}\frac{\sin nt}{n}$

We can write this $n$ into natural number and rename it into $k$ which I think look better:

$f(t)=\frac{4}{\pi}\sum_{k=1}^N\frac{\sin ((2k-1)t)}{2k-1}$