First-order Linear with Constant Coefficients: Behavior of Solutions, Use of Complex Methods.

June 4, 2019

(video 7-8)

Definite Integral

Let’s get the general solution for first order linear ODE with constant coefficients by integrating factors. For constant coefficients $p(t)=k$ , The integrating factor is $e^{\int kdt}=e^{kt}$

$\begin{align} y'+p(t)y&=q(t)\\ (ye^{kt})'&=e^{kt}q(t)\\ ye^{kt}&=\int e^{kt}q(t)+C\\ y&=e^{-kt}\int e^{kt}q(t)+Ce^{-kt}\\ \end{align}$

This is solved with indefinite integral. Sometimes people prefer definite integral because it is convenient for initial value substitution. Let’s see it.

$\begin{align} y'+p(t)y&=q(t)\\ (ye^{kt})'&=e^{kt}q(t)\\ y(t)e^{kt}-y(0)e^{0t}&=\int_0^t e^{kt}q(t)\\ y(t)&=e^{-kt}\int_0^t e^{kt}q(t)+y(0)e^{-kt}\\ y(t)&=e^{-kt}\int_0^t e^{kt}q(t)+y_0e^{-kt}\\ \end{align}$

You see that in this case we have $y_0=y(0)$ in the right hand side. This is the value when the function is at time 0, which is often known.

Steady-state Solution

This session we introduced a special form of first order linear ODE (sry the name is long) written in standard formthe standard form is $y'+p(t)y=q(t)$ :

$y'+ky=q(t)$

where $p(t)$ is a constant $k$ and does not change with input. The integrating factor $u=e^{\int kdt}=e^{kt}$ , then

$\begin{align} (ye^{kt})'&=e^{kt}q(t)\\ ye^{kt}&=\int e^{kt}q(t)\ dt+C\\ y&=\underbrace{e^{-kt}\int e^{kt}q(t)\ dt}_{steady-state\ solution}+\underbrace{Ce^{-kt}}_{\rightarrow0\ as\ t\rightarrow\infty\\transient} \end{align}$

The term $Ce^{-kt}$ goes to zero as $t$ goes to infinity, the rest is called steady-state solution or long-term solution. A steady-state solution means in the long-run, no matter what the initial value $C=y_0$ will be, the solution $y$ will converge to the steady-state solution.

Superposition of input

In brief, superposition of input is saying when we have input $q_1(t)$ , a response $y_1(t)$ and another response $q_2(t)$ and another output $y_2(t)$ . The input $q_1+q_2$ has the output $y_1+y_2$

Sinusoidal Input

Let’s have a special form of constant coefficient ODE:

$y'+ky=kq_e(t)$

A subscript $e$ is just a reminder that we have a constant $k$ on it. Since we have already seen a linear input, the temperature and concentration model in lecture3, this time let our input to be a cosine function:

$y'+ky=k*\cos(\omega t)\tag{1}$

where $\omega$ stands for the “angular frequency” or “# complete oscillations in 2 $\pi$ ”. To make the integration explicit, note that it’s not necessary to do this, we are going to “complexify” the problem by going into the complex domain. Remember

$\cos\theta+i\sin\theta=e^{i\theta}$

We will rewrite the problem (1) into

$\tilde y'+k\tilde y=k*e^{i\omega t}\tag{2}$

The reason we change $y$ into $\tilde y$ is because $\tilde y$ contains the real and imaginary solutions, turning into the “whole” solution, and we only need the real partproof to be added. An intuitive way to see this is by Superposition of input we feed in another imaginary input to (1). So

$\begin{align} \tilde y'+k\tilde y&=k*e^{i\omega t}\tag{2}\\ (\tilde ye^{kt})'&=k*e^{(k+i\omega )t}\\ \tilde ye^{kt}&=\frac{k}{k+i\omega}e^{(k+i\omega )t}\\ \tilde y&=\frac{1}{1+\frac{i\omega}{k}}e^{(i\omega )t}\\ \end{align}$

Now there’re two ways to separate this whole solution into a combo of real and complex. Last time when we multiply a complex conjugate of the denominator is by “going into” the Cartesian. Today we will go into polar. Before that we need to some properties of a complex number

Complex Properties

Let $\alpha=a+ib$ .

First and foremost, define $\alpha^{-1}$ s.t. $\alpha*\alpha^{-1}=1$ .

Proof: What’s $\alpha^{-1}$ ? Let $\alpha^{-1}=c+id$ , then
$\begin{array}{} \alpha\alpha^{-1}&=(a+ib)(c+id)\\ &=ac-bd+i(ad+bc)\\ \end{array}\tag{3}$
The real part is $ac-bd$ and the imaginary part is $ad+bc$ , we know that this two shall sum to 1, so
$\begin{array}{} ac-bd=1(1)\\ ad+cd=0(2) \end{array}\\ \begin{array}{} &(1)*-b:-abc+b^2d=-b\\ +&(2)*a:a^2+abc=0\\ \Rightarrow& a^2+b^2d=-b\\ \Rightarrow& d=\frac{-b}{a^2+b^2} \end{array}\\$
Similarly,
$\begin{array}{} &(1)*a:a^2c-abd=a\\ +&(2)*b:abd+b^2c=0\\ \Rightarrow& c=\frac{a}{a^2+b^2} \end{array}\\$
So at last,
$\begin{align} \alpha^{-1}&=\frac{a}{a^2+b^2}-\frac{b}{a^2+b^2}i\\ &=\frac{a-bi}{(a-bi)(a-bi)}\\ &=\frac{1}{a-bi}\\ &=\frac{1}{\alpha} \end{align}$
$\arg(\alpha\beta)=\arg(\alpha)+\arg(\beta)$ , for arbitrary complex number $\alpha=a+bi,\beta=c+di$

Proof: Similar to $\tan$ , $\arctan$ has the a similar property s.t.
$\tan^{-1}(\alpha)+\tan^{-1}(\beta)=\frac{\alpha+\beta}{1-\alpha\beta}$
From (3) we know product of any two complex number can be expressed that way, then the argument(angle) of $\alpha*\beta$ is
$\arg(\alpha\beta)=\tan^{-1}(\frac{ad+bc}{ac-bd})$
This is equal to
$\arg(\alpha)+\arg(\beta)=\tan^{-1}(\frac{b}{a})+\tan^{-1}(\frac{d}{c})$
$\arg(1/\alpha)=-\arg(\alpha)$
Proof: Let $\alpha=a+bi$ , then $\arg(\alpha)=\tan^{-1}(\frac{b}{a})$ . From the proof of 1 we see
$\alpha^{-1}=\frac{a}{a^2+b^2}-\frac{b}{a^2+b^2}i\\$
So
$\arg(1/\alpha)=\tan^{-1}(-\frac{b}{a})$
And $\arctan$ is an odd function.
$\arg(1/\alpha)+\arg(\alpha)=0$ .

Polar Form

Let’s back to our whole solution

$\tilde y=\frac{1}{1+\frac{i\omega}{k}}e^{(i\omega )t}$

Let’s take a look on the coefficient individually. Let $\phi$ be the angle of the denominator, that is, $\arg(1+\frac{\omega}{k}i)=\phi$ . Then $\arg(\frac{1}{1+\frac{\omega}{k}I})=-\phi$ . And the modulus $r$ is $\frac{1}{\sqrt{1+(\omega/k)^2}}$ . So we can express the coefficient as

$\frac{1}{\sqrt{1+(\omega/k)^2}}e^{-i\phi}$

Then

$\begin{align} \tilde y&=\frac{1}{\sqrt{1+(\omega/k)^2}}e^{-i\phi}*e^{i\omega t}\\ &=r*e^{i(\omega t-\phi)}\\ &\Rightarrow\\ y&=r*\cos(\omega t-\phi)\\ \end{align}$

$\phi=\tan^{-1}(\omega/k)$ is called the phase lag, the shift of the trigonometry function. And $r$ is the amplitude. $k$ is the conductivity. When $k$ goes up, $\phi$ goes down. Then the phase lag is smaller, it means we can get the response sooner(??? Not sure).

Cartesian Form

Let’s continue our problem. And we’re going to use the Cartesian form.

$\begin{align} \tilde y&=\frac{1}{1+\frac{i\omega}{k}}e^{(i\omega )t}\\ &=\frac{1-\frac{\omega}{k}i}{1+(\frac{\omega}{k})^2}(\cos\omega t+i\sin\omega t)\\ &\Rightarrow\frac{1}{1+(\omega/k)^2}(\cos\omega t+\frac{\omega}{k}\sin\omega t)\\ \end{align}\tag{1}$

This solution does not seem to correspond to our previous one, let’s work it out. One trick is that

Prop. 1

$a\cos\theta+b\sin\theta=C\cos(\theta-\phi)\tag{2}$

where $\phi=\tan^{-1}(\frac{b}{a})$ is the angle between $b$ and $a$ , and $C=\sqrt{a^2+b^2}$ .

Proof 1: First we can prove it by vectors. Remember $\phi$ is the angle between $b$ and $a$ . Then we have the following picture

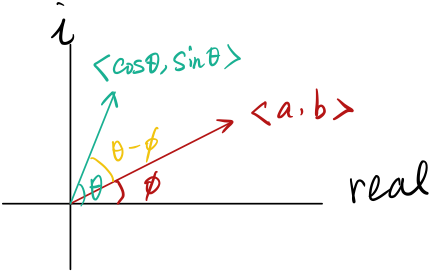
Let

$\begin{align} a\cos\theta+b\sin\theta&=<a,b>\cdot<\cos\theta,\sin\theta>\\ &=||<a,b>||*||<\cos\theta,\sin\theta>||*\cos(\theta-\phi)\\ &=C\cos(\theta-\phi) \end{align}$

We can also prove this by going into the complex domain. Still using Figure 1 to view the angles and modulus.

Proof 2:

$\begin{align} a\cos\theta+b\sin\theta&=Re((a-bi)(\cos\theta+i\sin\theta))\\ &=Re(\sqrt{a^2+b^2}e^{-i\phi}*e^{i\theta})\\ &=Re(Ce^{i(\theta-\phi)})\\ &=C\cos(\theta-\phi) \end{align}$

Then we can use the property right now.

$\begin{align} \tilde y&=\frac{1}{1+(\omega/k)^2}(\cos\omega t+\frac{\omega}{k}\sin\omega t)\\ &=\frac{1}{1+(\omega/k)^2}*\sqrt{1+(\omega/k)^2}\cos(\omega t-\phi)\\ &\Rightarrow\frac{1}{\sqrt{1+(\omega/k)^2}}\cos(\omega t-\phi) \end{align}$

where $\phi=\tan^{-1}(\omega/k)$ . Then we have the same solution as we did using polar form.