Complex Numbers and Complex Exponentials

June 3, 2019

Complex Conjugate

To do division, we multiply top and bottom by the denominator’s complex conjugate. For e.g.,

Polar Coordinate on Complex Numbers:

For an imaginary $\alpha=a+bi$

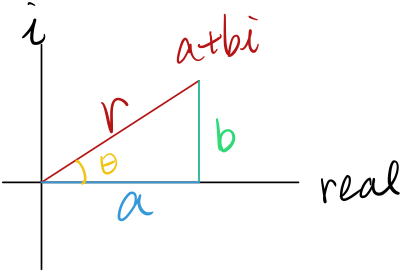
We can rewrite it into polar coordinates by letting $r=\sqrt{a^2+b^2}$ and $\theta=\tan^{-1}(\frac{b}{a})$,

The angle $\theta$ is called its ($\alpha$’s) argument, and the tangent line $r$ is called its modulus. And Euler discovered that

Rather than a proof it’s more like a definition. We just take it and use it here. If you’re interested in the proof, just expand both side of the equations by Taylor Series.

With the new expression, we can rewrite $\alpha$:

Writing a complex number in polar form is not just nice-looking but good for multiplication:

The modulus will be multiplied and the argument (angle) will be summed.

Let’s take an example:

We can view $\cos x$ as the real part of $e^{ix}$, that is,

we can add another $i\sin x$ to the equation to form it to $e^{ix}$, then (1) can become

And we want the real part of this, which will become clearer later.

We want the real part of this, not the imaginary part. One way to do that is by going into Cartesian, or multiply the complex conjugate of the denominator:

This works because of superposition of input which we will introduce on later notes.

Nth root of 1

? The video is unclear on this, will be added in the future